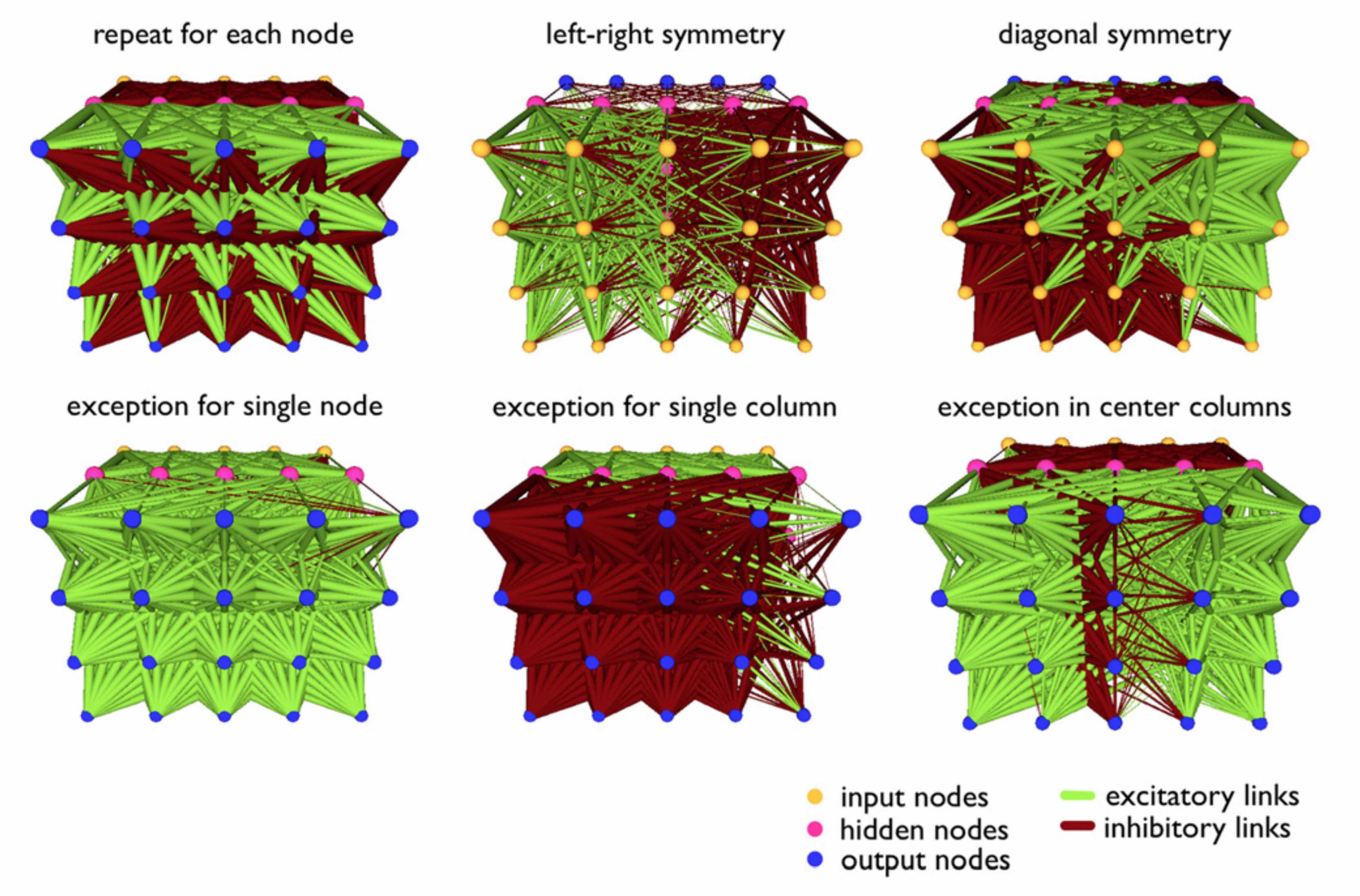
Examples of evolved self-attention agents
Neuroevolution of Self-Interpretable Agents
Abstract
Inattentional blindness is the psychological phenomenon that causes one to miss things in plain sight. It is a consequence of the selective attention in perception that lets us remain focused on important parts of our world without distraction from irrelevant details. Motivated by selective attention, we study the properties of artificial agents that perceive the world through the lens of a self-attention bottleneck. By constraining access to only a small fraction of the visual input, we show that their policies are directly interpretable in pixel space. We find neuroevolution ideal for training self-attention architectures for vision-based reinforcement learning tasks, allowing us to incorporate modules that can include discrete, non-differentiable operations which are useful for our agent. We argue that self-attention has similar properties as indirect encoding, in the sense that large implicit weight matrices are generated from a small number of key-query parameters, thus enabling our agent to solve challenging vision based tasks with at least 1000x fewer parameters than existing methods. Since our agent attends to only task-critical visual hints, they are able to generalize to environments where task irrelevant elements are modified while conventional methods fail.
Introduction
There is much discussion in the deep learning community about the generalization properties of large neural networks. While larger neural networks generalize better than smaller networks, the reason is not that they have more weight parameters, but as recent work (e.g.
Recent neuroscience critiques of deep learning (e.g.
There is actually a whole area of related research within the neurevolution field on evolving this genetic bottleneck, which is called an indirect encoding. Analogous to the pruning of lottery ticket solutions, indirect encoding methods allow for both the expressiveness of large neural architectures while minimizing the number of free model parameters. We believe that the foundations laid by the work on indirect encoding can help us gain a better understanding of the inductive biases
Most current methods used to train neural networks, whether with gradient descent or evolution strategies, aim to solve for the value of each individual weight parameter of a given neural network. We refer to these methods as direct encoding methods.
Indirect encoding
Before the popularity of Deep RL, indirect encoding methods in the neuroevolution literature have been a promising approach for the types of problems that eventually used Deep RL solutions.
In the case of vision-based RL problems, earlier works demonstrated that large neural networks can be encoded into much smaller, genotype solutions, that are capable of playing Atari from pixels
By encoding the weights of a large model with a small number of parameters, we can substantially reduce the search space of the solution, at the expense of restricting our solution to a small subspace of all possible solutions offered by direct encoding methods. This constraint naturally incorporates into our agent an inductive bias that determines what it does well at
In this work, we establish that self-attention can be viewed as a form of indirect encoding, which enables us to construct highly parameter-efficient agents.
We investigate the performance and generalization properties of these agents for vision-based RL tasks.
Self-attention has been popularized by Transformer
As we will show, neuroevolution is an ideal method for training self-attention agents, because not only can we remove unnecessary complexity required for gradient-based methods, resulting in much simpler architectures, we can also incorporate modules that enhance the effectiveness of self-attention that need not be differentiable. We showcase self-attention agents trained with neuroevolution that require 1000x fewer parameters than conventional methods and yet is able to solve challenging vision-based RL tasks. Specifically, with less than 4000 parameters, our self-attention agents can reach average scores of 914 over 100 consecutive trials in a 2D car racing task
The goal of this work is to showcase self-attention as a powerful tool for the neuroevolution toolbox, and we provide open-source code for reproducing our experiments (See Appendix). We hope our results will encourage further investigation into the neuroevolution of self-attention models, and also revitalize interest in indirect encoding methods.
Background on Self-Attention
We now give a brief overview of self-attention. Here, we describe a simpler subset of the full Transformer
Let be an input sequence of elements (e.g. number of words in a sentence, pixels in an image), each of dimensions (e.g. word embedding size, RGB intensities). Self-attention module calculates an attention score matrix and a weighted output:
where are matrices that map the input to components called Key and Query (), is the dimension of the transformed space and is usually a small integer.
Since the average value of the dot product grows with the vector's dimension, each entry in the Key and Query matrices can be disproportionally too large if is large. To counter this, the factor is used to normalize the inputs.
Applying the
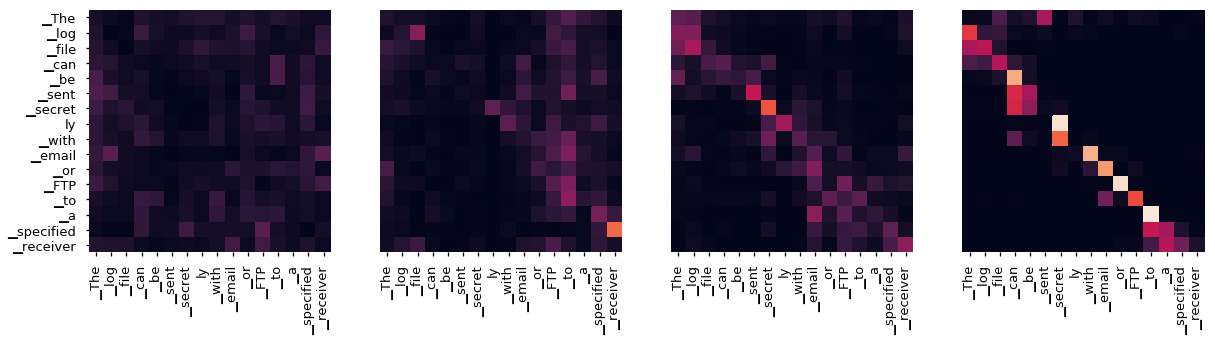
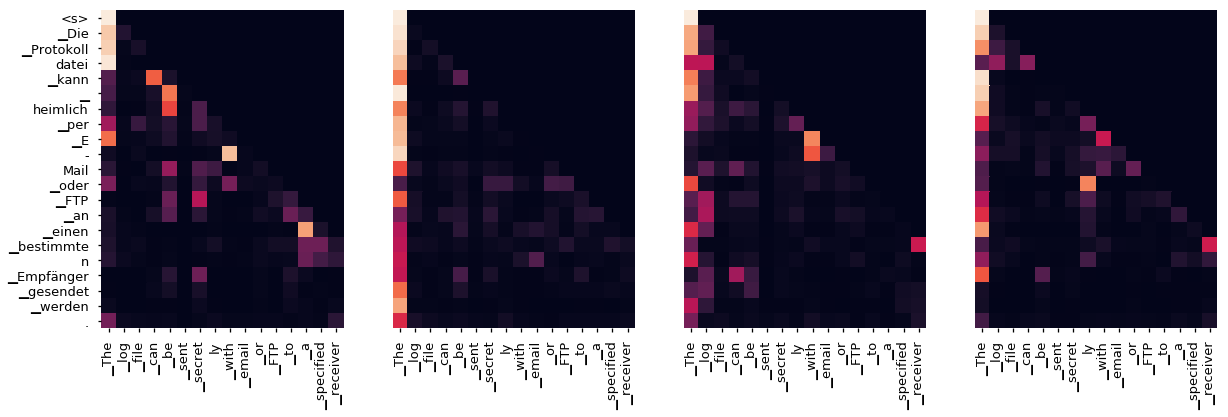
Self-attention lets us map arbitrary input to target output , and this mapping is determined by an attention matrix parameterized by much smaller Key and Query parameters, which can be trained using machine learning techniques. The self-attention mechanism is at the heart of recent SOTA methods for translation and language modeling
Self-Attention for Images
Although self-attention is broadly applied to sequential data, it is straightforward to adapt it to images.
For images, the input is a tensor where and are the height and width of the image, is the number of image channels (e.g., 3 for RGB, 1 for gray-scale).
If we reshape the image so that it becomes where and , all the operations defined in Equations 1-2 are valid and can be readily applied.
In the reshaped , each row represents a pixel and the attentions are between pixels. Notice that the complexity of Equation 1 grows quadratically with the number of rows in due to matrix multiplication, it therefore becomes computationally prohibitive when the input image is large.
While down-sampling the image before applying self-attention is a quick fix, it is accompanied with performance trade-off. For more discussion and methods to partially overcome this trade-off for images, see
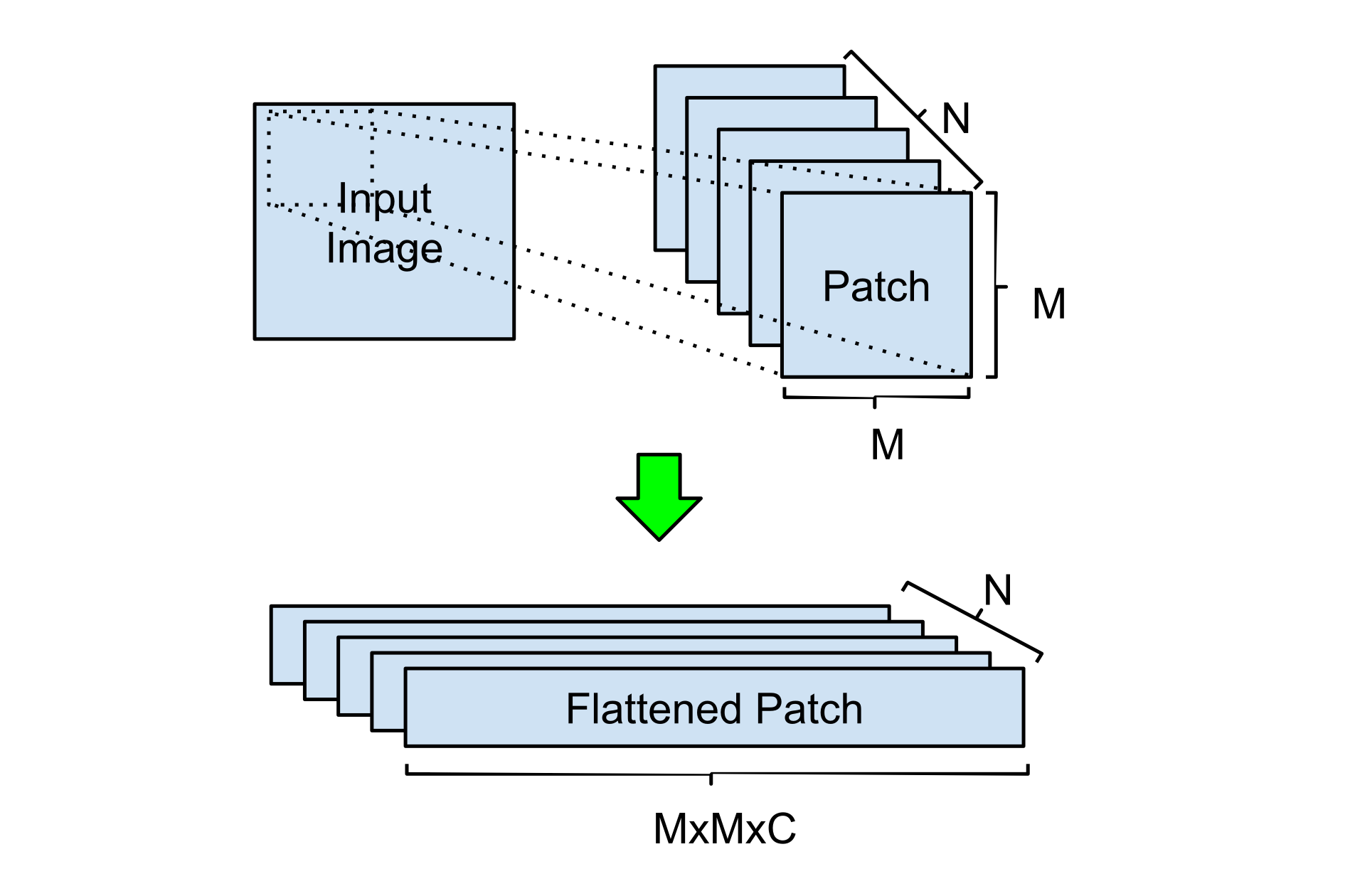
Instead of applying operations on individual pixels of the entire input, a popular method for image processing is to organize the image into patches and take them as inputs as described in previous work (e.g.
Self-Attention as a form of Indirect Encoding
Indirect encoding methods represent the weights of a neural network, the phenotype, with a smaller set of genotype parameters. How a genotype encodes a larger solution space is defined by the indirect encoding algorithm. HyperNEAT

|

|

|

|
|
|
Due to compression, the space of possible weights an indirect encoding scheme can produce is only a small subspace of all possible combination of weights. The constraint on the solution space resulting from indirect encoding enforces an inductive bias into the phenotype. While this bias determines the types of tasks that the network is naturally suited at doing, it also restricts the network to a subset of all possible tasks that an unconstrained phenotype can (in theory) perform. More recent works have proposed ways to broaden its task domain of indirect encoding. ES-HyperNEAT

Hypernetworks
Similarly, self-attention enforces a structure on the attention weight matrix in Equation 1 that makes it also input-dependent. If we remove the Key and Query terms, the outer product defines an association matrix
As the outer product so far has no free parameters, the corresponding matrix will not be suitable for arbitrary tasks beyond association. The role of the small Key () and Query () matrices in Equation 1 allow to be modified for the task at hand. and can be viewed as the genotype of this indirect-encoding method.
are the matrices that contain the free parameters, is a constant with image inputs (3 for RGB images and 1 for gray scale images), therefore the number of free parameters in self-attention is in the order of . As we explained previously, when applying self-attention to images can be the number of pixels in an input the magnitude of which is often tens of thousands even for small images (e.g. 100px × 100px). On the other hand, is the dimension of the transformed space in which the Key and Query matrices reside and is often much smaller than ( in our experiments). This form of indirect encoding enables us to represent the phenotype, the attention matrix , of size using only number of genotype parameters. In our experiments, we show that our attention matrix can be represented using only 1200 trainable genotype parameters.
Furthermore, we demonstrate that features from this attention matrix is especially useful to a downstream decision-making controller. We find that even if we restrict the size of our controller to only 2500 parameters, it can still solve challenging vision-based tasks by leveraging the information provided by self-attention.
Self-Attention Agent
The design of our agent takes inspiration from concepts related to inattentive blindness
The following figure depicts an overview of our self-attention agent:
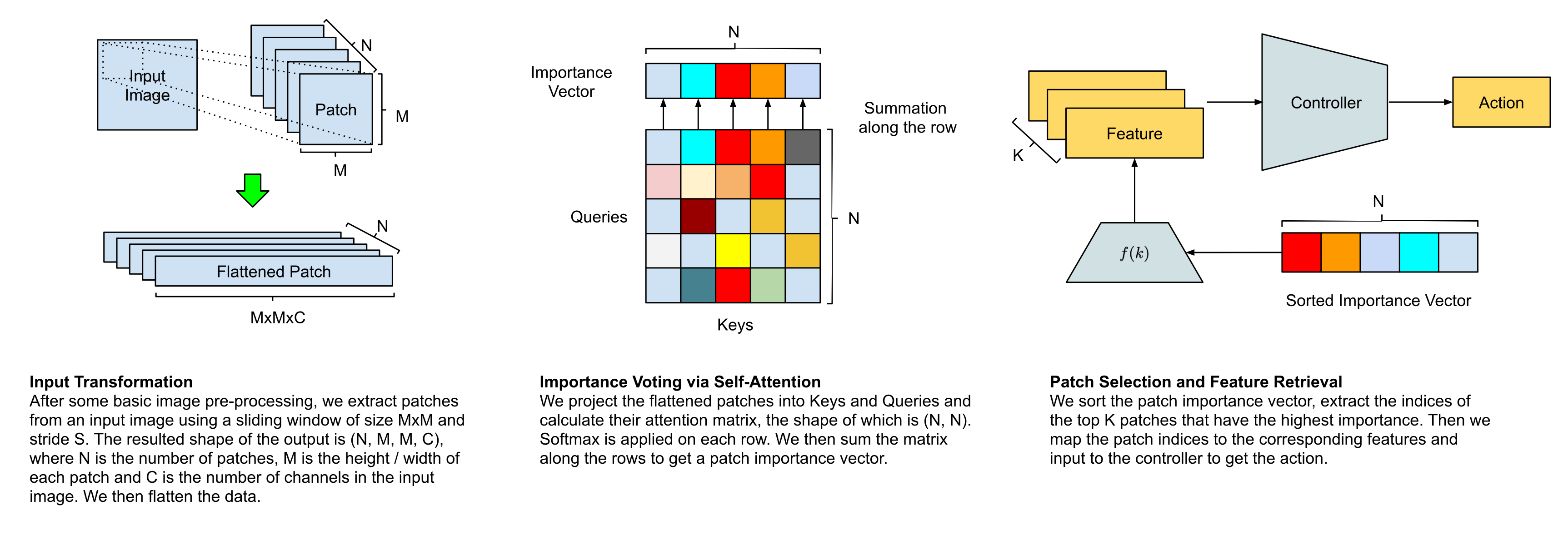
There are four stages of information processing:
Input Transformation Given an observation, our agent first resizes it into an input image of shape , the agent then segments the image into patches and regard each patch as a potential region to attend to.
Importance Voting via Self-Attention To decide which patches are appropriate, the agent passes the patches to the self-attention module to get a vector representing each patch's importance, based on which it selects patches of the highest importance.
Patch Selection and Feature Retrieval Our agent then uses the index () of each of the patches to fetch relevant features of each patch with a function , which can be either a learned module or a pre-defined function that incorporates domain knowledge.
Controller Finally, the agent inputs the features into its controller that outputs the action it will execute in its environment.
Each of these stages will be explained in greater detail in this section.
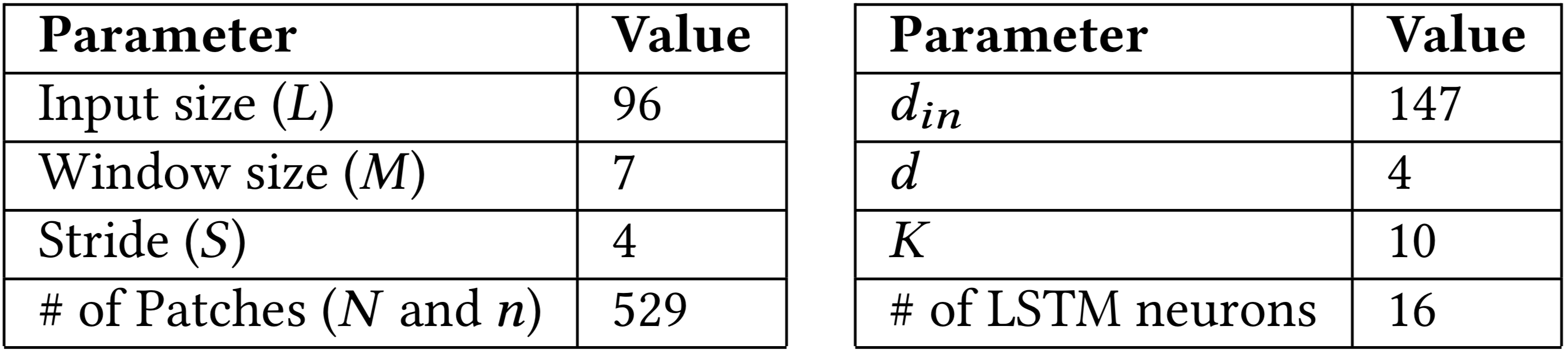
Hyper-parameters in this paper. Left: Parameters for input transformation. After resizing the observation into an image of shape L × L, we use a sliding window of specified size and stride to segment the image into patches. Right: Parameters for self-attention. Since the attention is between patches and each patch is RGB, we therefore have .
To gain a better sense of the magnitudes involved, we summarize the hyper-parameters used in this work in the table above. Some of the parameters are explained in the following sections.
Importance Voting via Self-Attention This module votes for the top K=10 patches (highlighted in white). (middle)
Patch Selection and Feature Retrieval Features from these K patches (such as location) routed to Controller. (right)
Input Transformation
Our agent does some basic image processing and then segments an input image into multiple patches. For all the experiments in this paper, our agent receives RGB images as its input, therefore we simply divide each pixel by 255 to normalize the data, but it should be straightforward to integrate other data preprocessing procedures. Similarly, while there can be various methods for image segmentation, we find a simple sliding window strategy to be sufficient for the tasks in this work.

To be concrete, when the window size and stride are specified, our agent chops an input of shape into a batch of patches of shape , where and are the height and width of the input image and is the number of channels. We then reshape the processed data into a matrix of shape before feeding it to the self-attention module. and are hyper-parameters to our model, they determine how large each patch is and whether patches overlap. In the extreme case when this becomes self-attention on each individual pixel in the image.
Importance Voting via Self-Attention
Upon receiving the transformed data in where and , the self-attention module follows Equation 1 to get the attention matrix of shape . To keep the agent as simple as possible, we do not use positional encoding in this work.
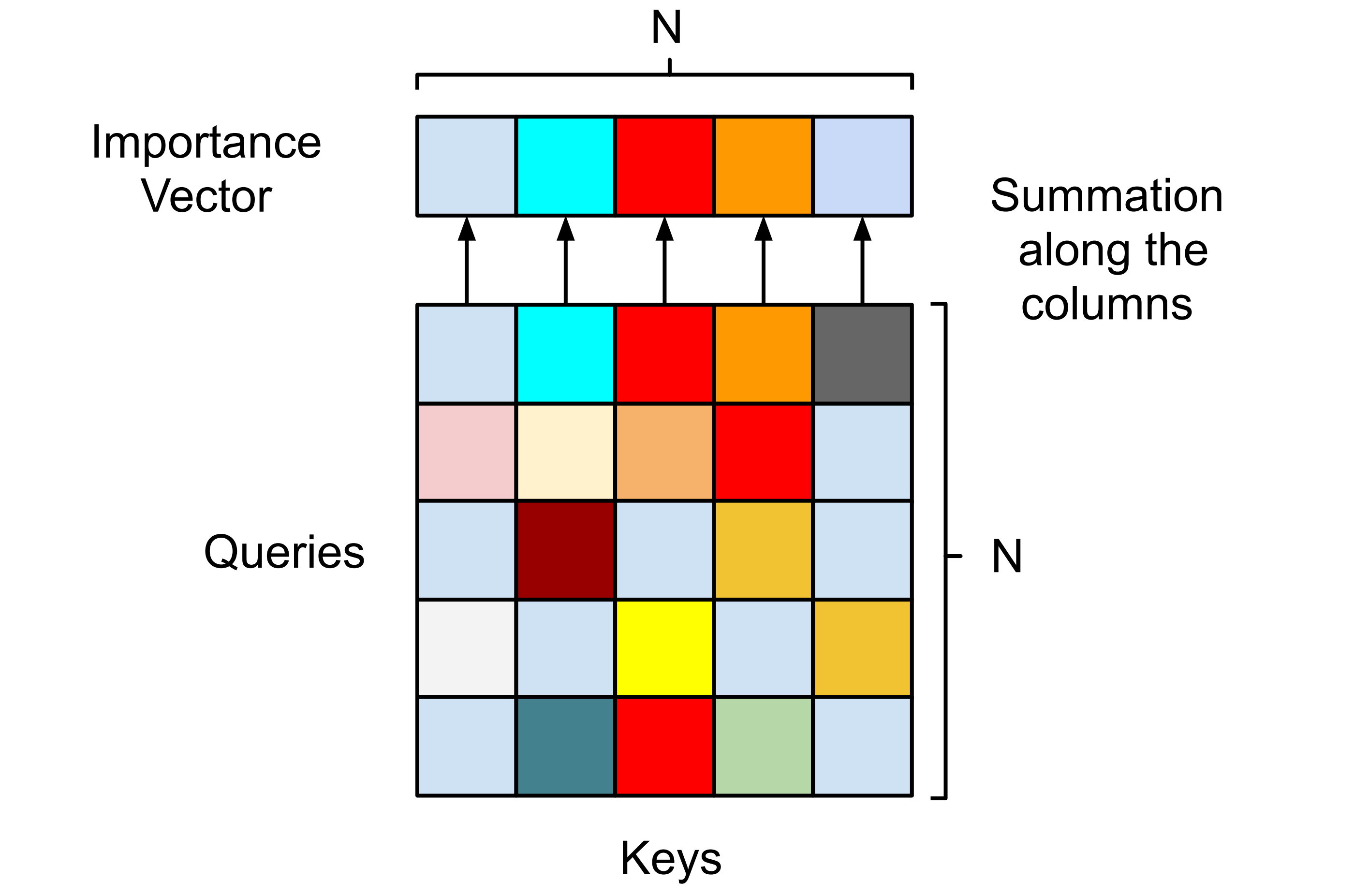
By applying softmax, each row in the attention matrix sums to one, so the attention matrix can be viewed as the results from a voting mechanism between the patches. To be specific, if each patch can distribute fractions of a total of 1 vote to other patches (including itself), row thus shows how patch has voted and column gives the votes that patch acquired from others. In this interpretation, entry in the attention matrix is then regarded as how important patch is from patch 's perspective. Taking sums along the columns of the attention matrix results in a vector that summarizes the total votes acquired by each patch, and we call this vector the patch importance vector. Unlike conventional self-attention, we rely solely on the patch importance vector and do not calculate a weighted output with Equation 2.
Patch Selection and Feature Retrieval
Based on the patch importance vector, our agent picks the patches with the highest importance. We pass in the index of these patches (denoted as index to reference the patch) into a feature retrieval operation to query the for their features. can be static mappings or learnable modules, and it returns the features related to the image region centered at patch 's position. The following list gives examples of possible features:
-
Patch center position. where the output contains the row and column indices of patch 's center position. This is the plain and simple method that we use in this work.
-
Patch's image histogram. where the output is the image histogram calculated from patch and is the number of bins.
-
Convolution layers' output. is a stack of convolution layers (learnable or fixed with pre-trained weights). It takes the image region centered at patch as input and outputs a tensor of shape .
The design choices of these features give us control over various aspects of the agent's capabilities, interpretability and computational efficiency.
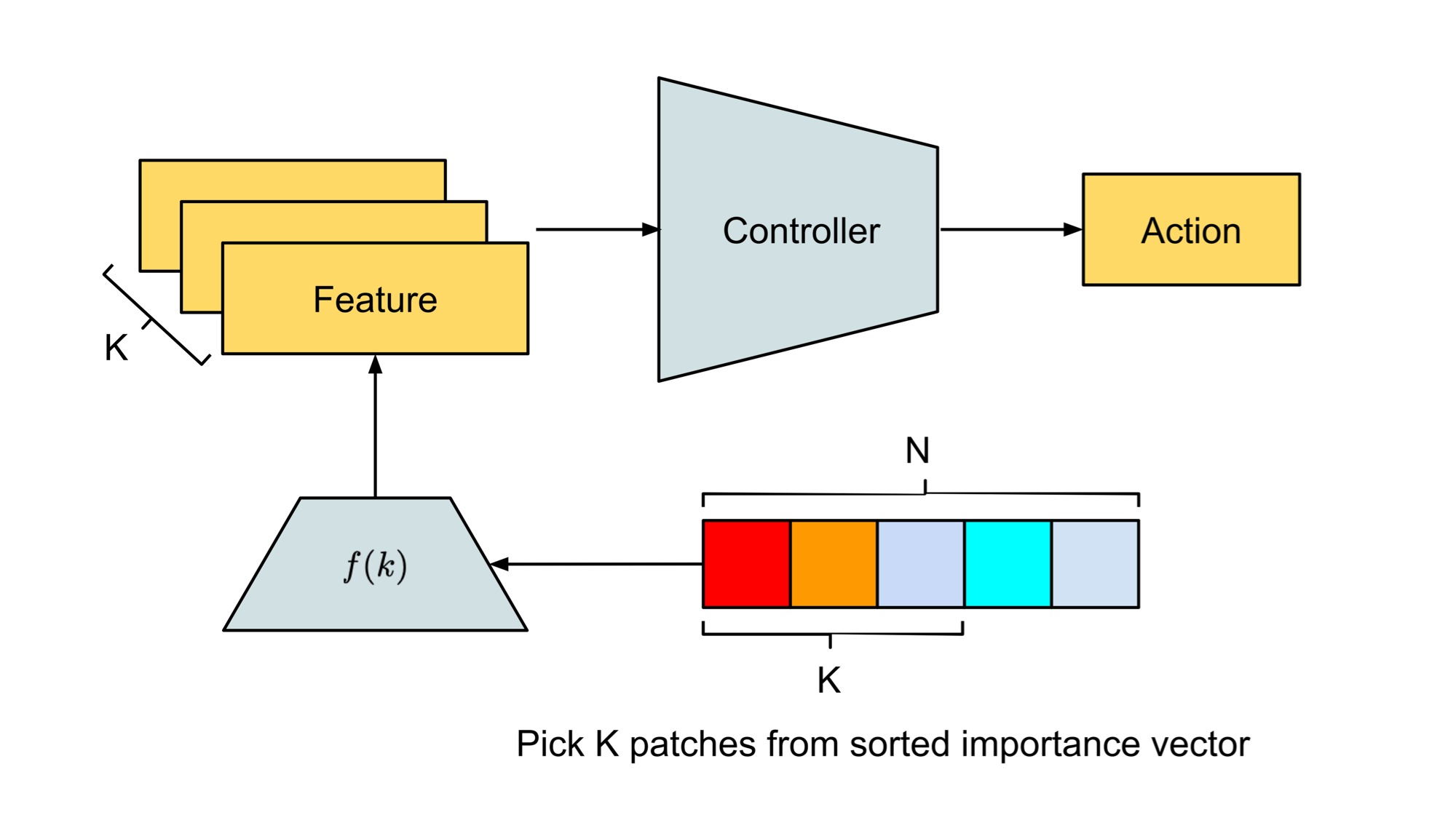
By discarding patches of low importance the agent becomes temporarily blind to other signals, this is built upon our premise and effectively creates a bottleneck that forces the agent to focus on patches only if they are critical to the task. Once learned, we can visualize the patches and see directly what the agent is attending to.
Although this mechanism introduces as a hyper-parameter, we find it easy to tune (along with and ). In principle we can also let neuroevolution decide on the number of patches, and we will leave this for future work.
Pruning less important patches also leads to the reduction of input features, so the agent is more efficient by solving tasks with fewer weights. Furthermore, correlating the feature retrieval operation with individual patches can also lower the computational cost. For instance, if some local features are known to be useful for the task yet computationally expensive, acts as a budget cap that limits our agent to compute features from only the most promising regions. Notice however, that this does not imply we permit only local features, as also has the flexibility to incorporate global features.
In this work, is a simple mapping from patch index to patch position in the image and is a local feature. But can also be a stack of convolution layers whose receptive fields are centered at patch . If the receptive fields are large enough, can provide global features.
Controller
Temporal information between steps is important to most RL tasks, but single RGB images as our input at each time step do not provide this information.
One option is to stack multiple input frames like what is done in
In our experiments, we use Long short-term memory (LSTM)
Neuroevolution of the Agent
Operators such as importance sorting and patch pruning in our proposed methods are not gradient friendly. It is not straightforward to apply back-propagation in the learning phase.
Furthermore, restricting to gradient based learning methods can prohibit the adoption of learnable feature retrieval functions that consist of discrete operations or need to produce discrete features.
We therefore turn to evolution algorithms to train our agent.
While it is possible to train our agent using any evolution strategy or genetic algorithms, empirically we find the performance of Covariance Matrix Adaptation Evolution Strategy (CMA-ES)
CMA-ES is an algorithm that adaptively increases or decreases the search space for the next generation given the current generation's fitness.
Concretely, CMA-ES not only adapts for the mean and standard deviation , but also calculates the entire covariance matrix of the parameter space.
This covariance matrix essentially allows us to either explore more by increasing the variance of our search space accordingly, or fine tune the solution when the collected fitness values indicate we are close to a good optima.
However the computation of this full covariance matrix is non-trivial, and because of this CMA-ES is rarely applied to problems in high-dimensional space
Experiments
We wish to answer the following questions via experiments and analysis:
-
Is our agent able to solve challenging vision-based RL tasks? What are the advantages over other methods that solved the same tasks?
-
How robust is the learned agent? If the agent is focusing on task-critical factors, does it generalize to the environments with modifications that are irrelevant to the core mission?
Task Description
We evaluate our method in two vision-based RL tasks: CarRacing
Right: Resized images presented to our agent as visual input, and also its attention highlighted in white patches.
In CarRacing, the agent controls three continuous actions (steering left/right, acceleration and brake) of the red car to visit as many randomly generated track tiles as possible in limited steps.
At each step, the agent receives a penalty of but will be rewarded with a score of for every track tile it visits where is the total number of tiles.
Each episode ends either when all the track tiles are visited or when 1000 steps have passed.
CarRacing is considered solved if the average score over 100 consecutive test episodes is higher than 900.
Numerous works have tried to tackle this task with Deep RL algorithms,
but has not been solved until recently by methods we will refer to as
VizDoom serves as a platform for the development of agents that play DOOM using visual information. DoomTakeCover is a task in VizDoom where the agent is required to dodge the fireballs launched by the monsters and stay alive for as long as possible.
Each episode lasts for 2100 steps but ends early if the agent dies from being shot.
This is a discrete control problem where the agent can choose to move left/right or stay still at each step.
The agent gets a reward of for each step it survives, and the task is regarded solved if the average accumulated reward over 100 episodes is larger than 750.
While a pre-trained
The above figure shows our network architecture and related parameters. We resize the input images to and use the same architecture for both CarRacing and DoomTakeCover (except for the output dimensions). We use a sliding window of size and stride to segment the input image, this gives us patches. After reshaping, we get an input matrix of shape . We project the input matrix to Key and Query with , after self-attention is applied we extract features from the most importance patches and input to the single layer LSTM controller (#hidden=16) to get the action.
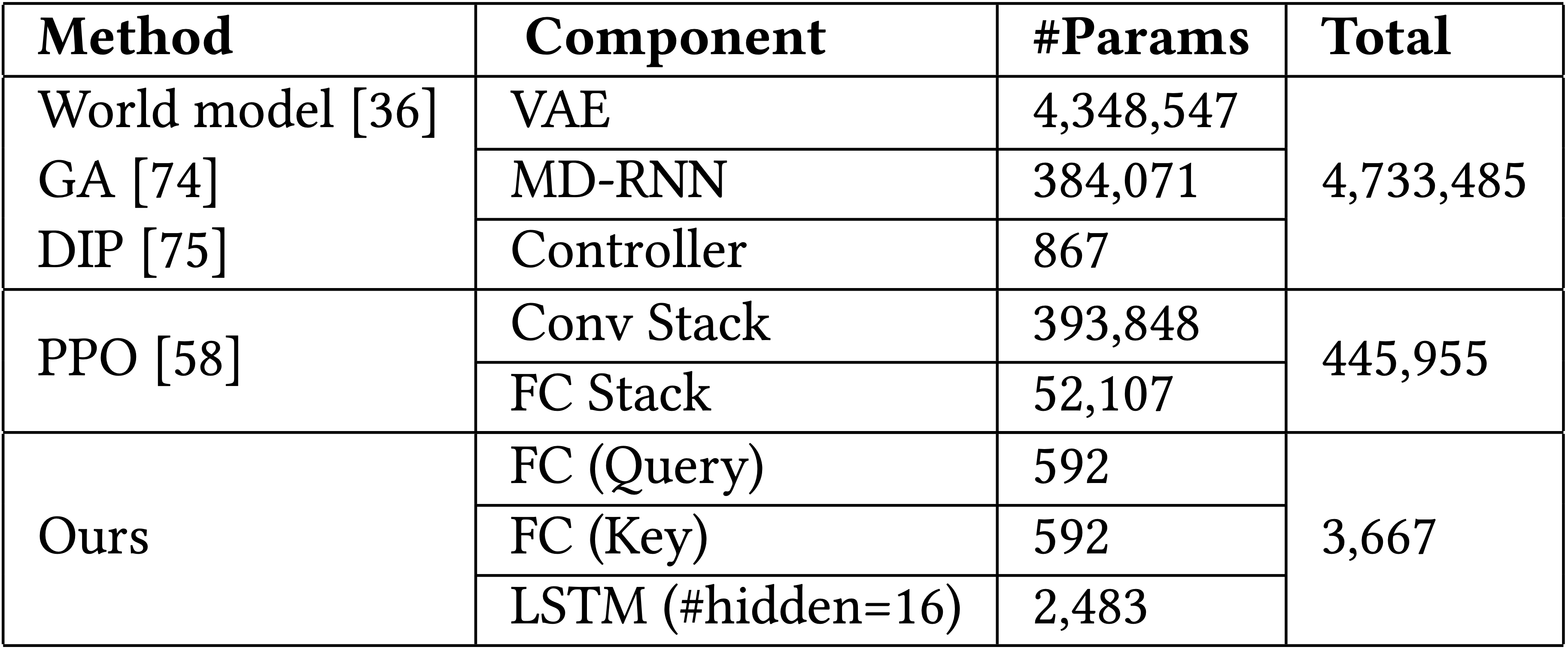
The table above summarizes the number of parameters in our agent, we have also included models from some existing works for the purpose of comparison.
For feature retrieval function , we use a simple mapping from patch index to patch center position in the input image.
We normalize the positions by dividing the largest possible value so that each coordinate is between 0 and 1. In our experiments, we use pycma
Experimental Results
Not only is our agent able to solve both tasks, it also outperformed existing methods. Here is a summary of our agent's results:
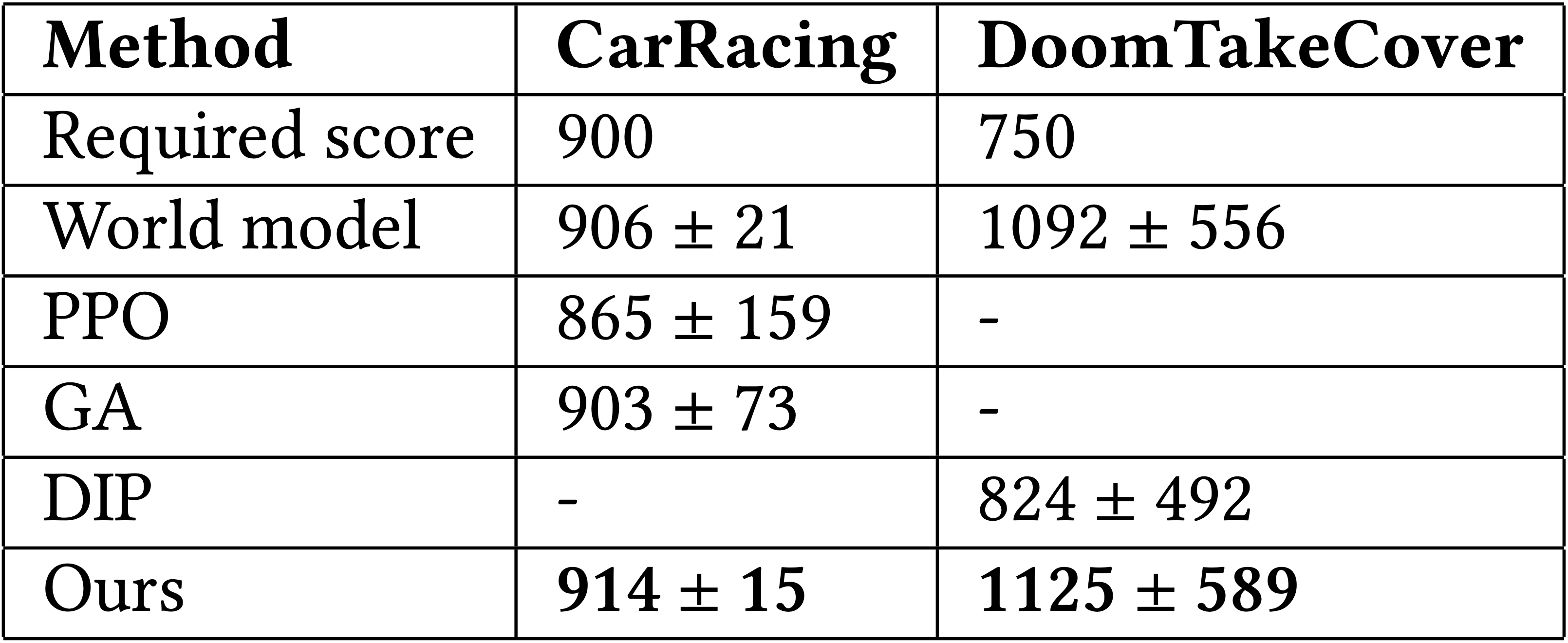
Test scores vs training iterations. We test our agent for 100 consecutive episodes with different environment seeds every 10 training iterations. The solid line shows the average score, the shaded area gives the standard deviation, and the dashed line indicates the score above which the task is considered solved.
In addition to the SOTA scores, the attention patches visualized in pixel space also make it easier for humans to understand the decisions made by our agent. Here, we visualize our agent's attention by plotting the top important patches elected by the self-attention module on top of the input image and see directly what the agent is attending to (the opacity indicates the importance, the whiter the more important):
From visualizing the patches and observing the agent's attention, we notice that most of the patches the agent attends to are consistent with humans intuition. For example, in CarRacing, the agent's attention is on the border of the road but shifts its focus to the turns before the car needs to change its heading direction. Notice the attentions are mostly on the left side of the road. This makes sense from a statistical point of view considering that the racing lane forms a closed loop and the car is always running in a counter-clockwise direction.
In DoomTakeCover, the agent is able to focus its attention on fireballs. When the agent is near the corner of the room, it is also able to detect the wall and change its dodging strategy instead of stuck into the dead end. Notice the agent also distributes its attention on the panel at the bottom, especially on the profile photo in the middle. We suspect this is because the controller is using patch positions as its input, and it learned to use these points as anchors to estimate its distances to the fireballs.
We also notice that the scores from all methods have large variance in DoomTakeCover. This seems to be caused by the environment’s design: some fireballs might be out of the agent’s sight but are actually approaching. The agent can still be hit by the fireballs outside its vision when it’s dodging other fireballs that are in the vision.
Through these tasks, we are able to give a positive answer to the first question: Is our agent able to solve challenging vision-based RL tasks? What are the advantages over other methods that solved the same tasks? Our agent is indeed able to solve these vision-based RL challenges. Furthermore, it is efficient in terms of being able to reach higher scores with significantly fewer parameters.
Region of Interest to Importance Mapping
Our feature retrieval function is a simple mapping from patch index to (normalized) positions of the patch's center point. As such, this function provides information only about the locations of the patches, and discards the content inside these patches.
On first thought, it is actually really surprising to us that the agent is able to solve tasks with the position information alone. But after taking a closer look at the contents of the patches that the agent attends to, it is revealed that the agent learns not only where but also what to attend to. This is because the self-attention module, top patch selection, and the controller are all trained together as one system.
To illustrate this, we plot the histogram of patch importance that are in the top quantile from 20 test episodes. Although each episode presents different environmental randomness controlled by their random seeds at initialization, the distributions of the patch importance are quite consistent, this suggests our agent's behavior is coherent and stable. When sampling and plotting patches whose importance are in the specified ranges, we find that the agent is able to map regions of interest (ROI) to higher importance values.
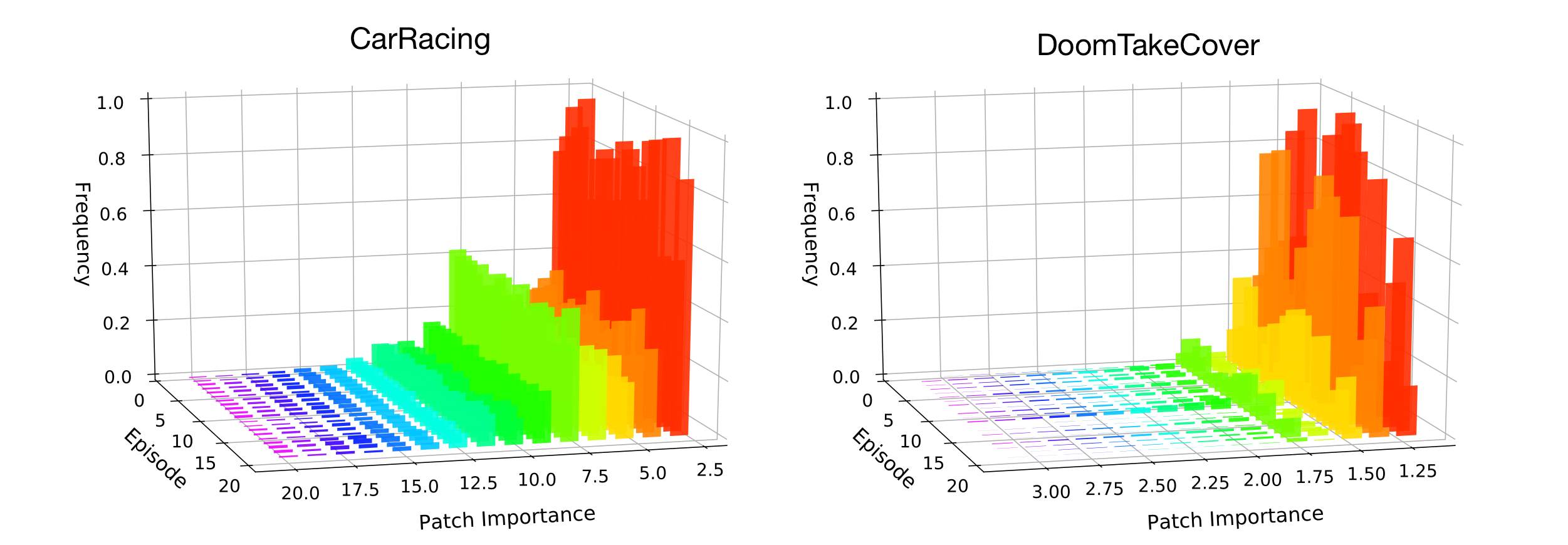
Importance voting mechanism via self-attention is able to identify a small minority of patches that are important for the task. The histogram shows the importance distribution of patches from 20 test episodes by patch importance scores. (Click Image to Enlarge)

The patches of the highest importance are those critical to the core mission. These are the patches containing the red and white markers at the turns in CarRacing and the patches having fires in DoomTakeCover (patches on the left). Shifting to the range that is around the quantile, the patch samples are not as interesting as before but still contains useful information such as the border of the road in CarRacing and the texture of walls in DoomTakeCover. If we take an extreme and look at the patches with close to zero importance (patches on the right), those patches are mostly featureless and indeed have little information.
By mapping ROIs to importance values, the agent is able to segment and discriminate the input to its controller and learn what the objects are it is attending to. In other words, the self-attention module learns what is important to attend to and simply gives only the (normalized) positions of the top things in the scene to the controller. As the entire system is evolved together, the controller is still able to output reasonable actions based only on position information alone.
Can our agents generalize to unseen environments?
To test our agent's robustness and its ability to generalize to novel states, we test pre-trained agents in modified versions of CarRacing and DoomTakeCover environments without re-training or fine-tuning them. While there are infinitely many ways to modify an environment, our modifications respect one important principle: the modifications should not cause changes of the core mission or critical information loss. With this design principle in mind, we present the following modifications:
- CarRacing--Color Perturbation We randomly perturb the background color. At the beginning of each episode, we sample two scalar perturbations uniformly from the interval and add respectively to the lane and grass field RGB vectors. Once the perturbation is added, the colors remain constant throughout the episode.
- CarRacing--Vertical Frames We add black vertical bars to both sides of the screen. The window size of CarRacing is 800px × 1000px. We add two vertical bars of width 75px on the two sides of the window.
- CarRacing--Background Blob We add a red blob at a fixed position relative to the car. In CarRacing, as the lane is a closed loop and the car is designed to run in the counter clock-wise direction, the blob is placed to the north east of the car to reduce lane occlusion.
- DoomTakeCover--Higher Walls We make the walls higher and keep all other settings the same.
Left: Rendering of modified game environment. Center: Agent's visual input. Right: Reconstruction of what the baseline agent actually sees, based on its World Model trained only on the original environment.
- DoomTakeCover--Different Floor Texture We change the texture of the floor and keep all other settings the same.
Left: Rendering of modified game environment. Center: Agent's visual input. Right: Reconstruction of what the baseline agent actually sees, based on its World Model trained only on the original environment.
- DoomTakeCover--Hovering Text We place a blue blob containing text on top part of the screen. The blob is placed to make sure no task-critical visual information is occluded.
Left: Rendering of modified game environment. Center: Agent's visual input. Right: Reconstruction of what the baseline agent actually sees, based on its World Model trained only on the original environment.
For the purpose of comparison, we used the released code (and pre-trained models, if available) from
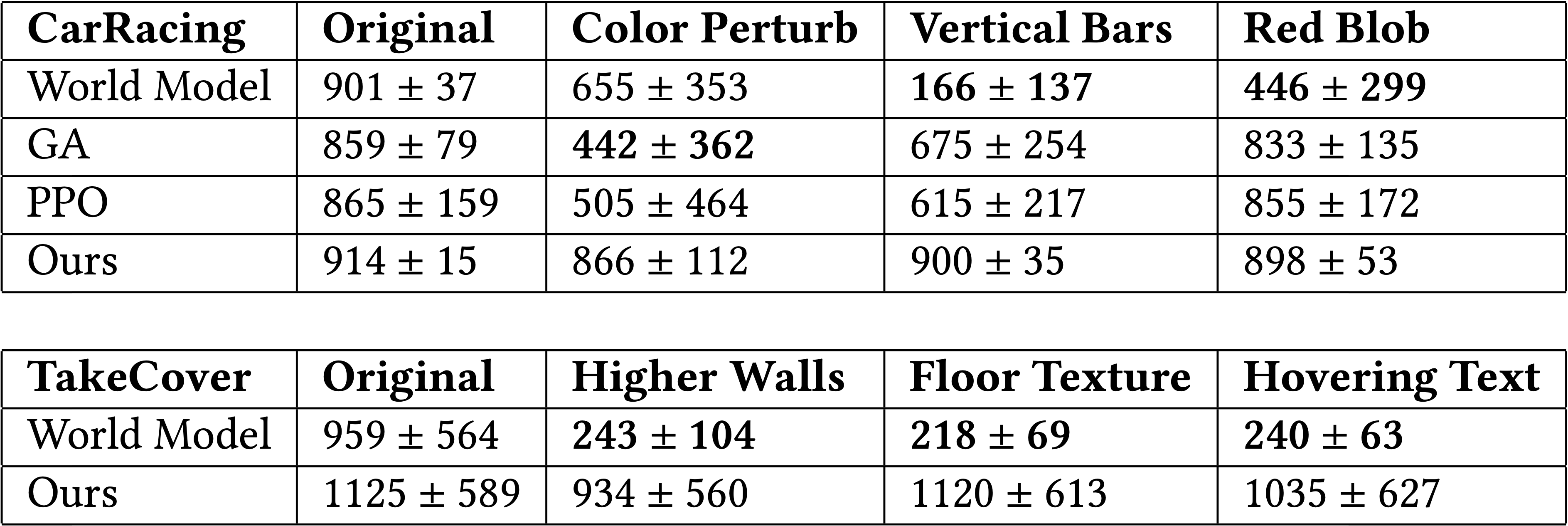
Our agent generalizes well to all modifications while the baselines fail. While World Model does not suffer a significant performance loss in color perturbations in CarRacing, it is sensitive to all changes. Specifically, we observe score drops in Vertical Frames, Higher Walls, Floor Texture, Hovering Text and a score drop in Background Blob from its performances in the unmodified tasks.
Since World Model's controller used as input the abstract representations it learned from reconstructing the input images, without much regularization, it is likely that the learned representations will encode visual information that is crucial to image reconstruction but not task-critical. If this visual information to be encoded is modified in the input space, the model produces misleading representations for the controller and we see performance drop.
In contrast, GA and PPO performed better at generalization tests. The end-to-end training may have resulted in better task-specific representations learned compared to World model, which uses an unsupervised representation based data collected from random policies. Both GA and PPO can fine-tune their perception layers to assign greater importance to particular regions via weight learning.
Through these tests, we are able to answer the second question posed earlier: How robust is the learned agent? If the agent is focusing on task-critical factors, does it generalize to the environments with modifications that are irrelevant to the core mission?
The small change in performance shows that our agent is robust to modifications. Unlike baseline methods that are subject to visual distractions, our agent focuses only on task-critical positions, and simply relies on the coordinates of small patches of its visual input identified via self-attention, and is still able to keep its performance in the modified tasks without any re-training. By learning to ignore parts of the visual input that it deems irrelevant, it can naturally still perform its task even when irrelevant parts of its environment are modified.
Related Work
Our work has connections to work in various areas:
Neuroscience Although the human visual processing mechanisms are not yet completely understood, recent findings from anatomical and physiological studies in monkeys suggest that visual signals are fed into processing systems to extract high level concepts such as shape, color and spatial organization
A line of work that narrows the gap is World Models
While we do not fully understand the mechanisms of how our brains develop abstract representations of the world, it is believed that attention is the unconscious mechanism by which we can only attend to a few selected senses at a time, allowing our consciousness to condense sensory information into a synthetic code that is compact enough to be carried forward in time for decision making
Neuroevolution-based methods for tackling challenging RL tasks have recently gained popularity due to their simplicity and competitiveness to Deep RL methods, even on vision-based RL benchmark tasks
It is worthy to note that even before the popularity of deep RL-based approaches for vision-based tasks, indirect encoding methods from the neuroevolution literature have been used to tackle challenging vision-based tasks such as Atari domain
Indirect encoding methods are not confined to neuroevolution. Inspired by earlier works
Attention-based RL Inspired by biological vision systems, earlier works formulated the problem of visual attention as an RL problem
In order to capture the interactions in a system that affects the dynamics,
In addition to these works, attention is also explicitly used for interpretability in RL.
In
Although these methods brought exciting results, they need dedicated network architectures and carefully designed training schemes to work in an RL context.
For example,
The high dimensionality the visual input makes it computationally prohibitive to apply attention directly to individual pixels, and we rather operate on image patches (which have lower dimensions) instead. Although not in the context of self-attention, previous work (e.g.
Discussion
While the method presented is able to cope with various out-of-domain modifications of the environment, there are limitations to this approach, and much more work to be done to further enhance the generalization capabilities of our agent. We highlight some of the limitations of the current approach in this section.
Much of the extra generalization capability is due to attending to the right thing, rather than from logical reasoning. For instance, if we modify the environment by adding a parallel lane next to the true lane, the agent attends to the other lane and drives there instead. Most human drivers do not drive on the opposite lane, unless they travel to another country.
We also want to highlight that the visual module does not generalize to cases where dramatic background changes are involved.
Inspired by
The agent trained on the original environment with the green grass background fails to generalize when the background is replaced with distracting YouTube videos. When we take this one step further and replace the background with pure uniform noise, we observe that the agent's attention module breaks down and attends only to random patches of noise, rather than to the road-related patches.
Left: The policy trained on the normal environment does not transfer to the noisy environment (Score: -58±12)
Right: Agent trained from scratch in this noisy environment (Score: 577±243)
When we train an agent from scratch in the noisy background environment, it still manages to get around the track, although the performance is mediocre. Interestingly, the self-attention layer still attends only to the noise, rather than to the road, and it appears that the controller actually learns a policy to avoid such locations!
We also experiment with various (the number of patches). Perhaps lowering the number will force the agent to focus on the road. But when we decrease from 10 to 5 (or even less), the agent still attends to noisy patches rather than to the road. Not surprisingly, as we increase to 20 or even 30, the performance of this noise-avoiding policy increases.
These results suggest that while our current method is able to generalize to minor modifications of the environment, there is much work to be done to approach human-level generalization abilities. The simplistic choice we make to only use the patch locations (rather than their contents) may be inadequate for more complicated tasks. How we can learn more meaningful features, and perhaps even extract symbolic information from the visual input will be an exciting future direction.
Conclusion
The paper demonstrated that self-attention is a powerful module for creating RL agents that is capable of solving challenging vision-based tasks. Our agent achieves competitive results on CarRacing and DoomTakeCover with significantly fewer parameters than conventional methods, and is easily interpretable in pixel space. Trained with neuroevolution, the agent learned to devote most of its attention to visual hints that are task-critical and is therefore able to generalize to environments where task irrelevant elements are modified while conventional methods fail.
Yet, our agent is nowhere close to generalization capabilities of humans. The modifications to the environments in our experiments are catered to attention-based methods. In particular, we have not modified properties of objects of interest, where our method may perform as poorly (or worse) than methods that do not require sparse attention in pixel space. We believe this work complements other approaches (e.g.
Neuroevolution is a powerful toolbox for training intelligent agents, yet its adoption in RL is limited because its effectiveness when applied to large deep models was not clear until only recently
In this work, we also establish the connections between indirect encoding methods and self-attention. Specifically, we show that self-attention can be viewed as a form of indirect encoding. Another interesting direction for future works is therefore to explore other forms of indirect encoding bottlenecks that, when combined with neuroevolution, can produce parameter efficient RL agents exhibiting interesting innate behaviors.

 This work has been presented at
This work has been presented at